3重解 グラフ 137412-3重解 グラフ

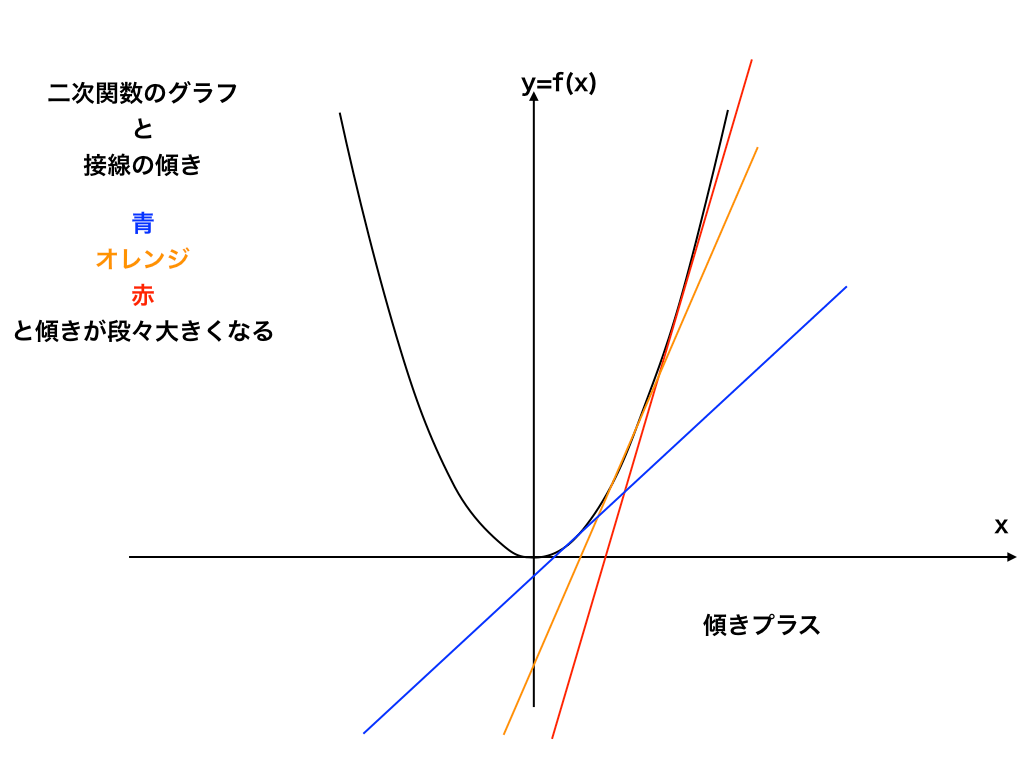
 接点と重解 ちなみに、放物線と直線が接する場合は、実数解が1つということなので、重解となります。二次関数の場合は、これを使い、判別式が $0$ であることを利用して解くこともできます（参考：標準二次関数のグラフと直線との共有点）。 三次関数の場合は、接点の x 座標が3次曲線は、変曲点を1つもち、その座標は 3 2 2 2 9 27, 3 27 b b abc a d a a である。 3次曲線は、変曲点が存在す れば、極大点・極小点は変曲点 に関して対象である。 いいかえれば、極大値と極小値 を持つとき、変曲点は極大値と2 3 ( ) ( ) ( ) ( ) S ¯ ® ­ 16 2 次方程式 ax2 bx c 2 0 が重解を もつとき，判別式 D b2 4ac ( ① 0) である。 また， そのときの重解は，x ( ② ) 24 軸公式 で 17 次の2 次方程式が重解をもつように，定 数 m の値を定め，そのと きの重解を 求めよ。 2x2 mx 1 0 解） 重解を

標準 四次関数と微分 なかけんの数学ノート

3重解 グラフ

3重解 グラフ-小野測器減衰をあらわす係数の意味と求め方 (page1) 1 はじめに 機械が稼働していれば振動は避けられない現象ですが、振動は不快なだけでなく故障の原因ともなり、甚だしい場合には機械の破壊に至ることもあります。 振動が起きてから対策を施していY=a (x−α) (x−α) (x−α)=a (x−α) 3 のグラフはDのようになります． 例えば， α=2, β=2, γ=2 の場合，方程式は y=a (x−2) 3 となり，上のDの図になります． x 3 の係数 a が負の値の場合，例えば y=− (x−2) 3 のときは，下のDの図になります． ** これらの場合も，グラフは x=α (=β=γ) の所で「接点」となり，しかもその後向こう側に出ます．** ≪解説図≫ ※三重解を持つDの

高校数学 直線と放物線の共有点の分類 映像授業のtry It トライイット

3次関数の増減問題を，2次方程式の解の配置問題にしてしまう． 実習2 3次関数 y=x 3 x 2 ax のグラフが 0≦x≦1 の区間で単調増加となるような定数 a の値の範囲を求めてください． 右の≪図2≫に示した曲線は y=x 3 x 2 ax のグラフです． 縦のスケールを適当にクリックして a の値を変え， 0≦x≦1 の区間で単調増加となるような定数 a の値の見当を付けてください ②のときグラフと\(x\)軸はただ1つの点で交わることになりますが、その\(x\)座標は、2次方程式の重解となります。この場合、グラフと\(x\)軸は 接する といい、共有点を 接点 といいます。考え方は難しくありませんが計算に工夫が必要です。 解答 与えられた四次関数と y = A x B y=AxB y = Ax B が x = α, β x=\alpha,\\beta x = α, β で接するとき， x 4 − 2 x 3 1 − A x − B = ( x − α) 2 ( x − β) 2 x^42x^31AxB= (x\alpha)^2 (x\beta)^2 x4 −2x3 1− Ax −B = (x− α)2(x −β)2

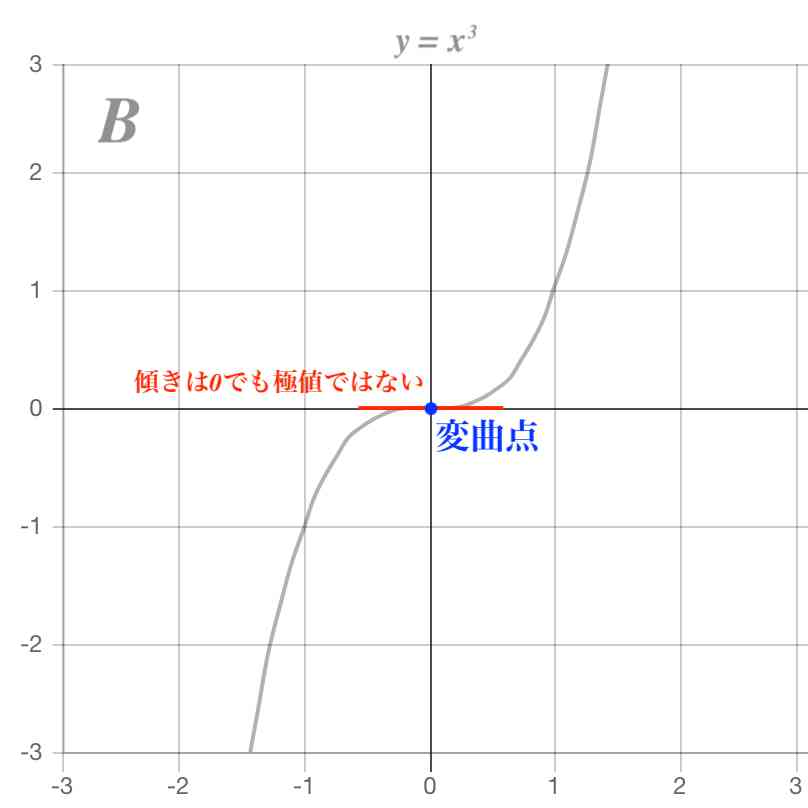
\( x=2\) は重解です。 3次方程式は複素数の範囲で重解を含めて3つの解を持ちます。 このように因数定理を用いて因数分解する方法が高次方程式の解き方です。 不等式の解き方を見れば分かりますが、グラフで見れば\(\,x\,\)軸との交点が方程式の解です。まず，2次関数 \(y = x^2 4x 3\) のグラフをノートに描いてください。 描けましたか？ 描けたら，下の 入力ボックス に式「x^2 4x 3」を入力してください。 \(y = x^2 4x 3\) のグラフが描かれます。 \(y = \) 勿論，皆さんが描いたグラフと同じになっているはずです。 と言う事でしょうか？x=αで3重解を持つならそのような3次式は f(x)=(xα)^3 ですから f'(x)=3(xα)^2, f''(x)=6(xα) ですのでf(α)=f'(α)=f''(α)=0 は明らかですし、 f''(x)がxの一次式で、f''(α)=0 なので f''(x)=k(xα) f'(x)=k/2*(xα)^2C f(x)=k/6*(xα)^3CxC'

 x（x^2＋9x＋126k）＝0が重解を持てばよいから、次の2通りがある。 (1) この方程式が、x＝0を重解に持つ時、k＝2から、他の解は 9となり題意を満たす。 (2) x^2＋9x＋126k＝0が重解を持ち、その解が0と異なる時、判別式＝0より k＝11/8この時、重解は 9/2 微分を使わない別解。 y＝ (1/6)x^3 (3/2)x^22x と y＝kx の接点をα、他の交点をβとする。 (1/6)x^3 (3 三次関数のグラフは、最大 \(1\) 個ずつの山と谷をもち、両端が正負逆方向に伸びる曲線です（山・谷をもたない場合もあり）。 グラフの向きは、\(x^3\) の係数 \(a\) の正負によって決まりN 2 N に対して、a1n は方程式xn = a の正の実数解を表わす。 n = 2m1 が奇数のときは

極値をもつために異なる二つの実数解を持つこと と書かれているのですが 一つの実数解で Clear

4次関数が極値をもたない条件で 1 の重解または虚数解をもつときでな Yahoo 知恵袋

詳細は先ほどのサイトに。 かつ のとき ことなる実数解3つが存在する。1つ目の実数解 を用いると、解き では上の3つを幾何、すなわちグラフとして示してみよう。「異なる二つの実数解」の場合、二次関数\( f(x) \)とx軸の交点が解のそれぞれの値となっている。「重解」の場合は、二次関数\( f(x) \)とx軸の接点が解の値となっている。71 ⑴ 𝛼𝛽=3，𝛼𝛽=5 (𝛼−1)(𝛽−1)=1，(𝛼−1)(𝛽−1)=3 より 𝑥 6−𝑥3=0 ⑵ 2𝛼2𝛽=6，2𝛼∙2𝛽= より 6𝑥−6𝑥=0 ⑶ (𝛼𝛽)𝛼𝛽=8，(𝛼𝛽)𝛼𝛽=15 より 𝑥 6−8𝑥15=0 72 係数が実数だから 1−2𝑖 が解のとき 12𝑖 も解である。

微分の質問です こちらの問題なのですが Clear

標準 四次関数と微分 なかけんの数学ノート

− 91 − 高校講座・学習メモ 数学Ⅰ 2次関数のグラフと2次不等式 ⑵ ポイント2 x軸と共有点のない2次関数Y'=0 の実数解は x=1 ， x=2 (3重解) となるが， x=2 では y'=0 となって， x=2 の前後で符号は変化する． 符号が3回変化する（1回と同じ）と考えてもよい． ただし， x=2 では y'=0 となるので，接線の傾きは一度 0 になる． 増減表は次のようになる． y=··· b 2 c 24ac 34b 3 d27a 2 d 2 18abcd と覚えるに値しない複雑な結果となります。 この判別式Dの値が D>0⇒異なる実数解3個 D=0⇒重解（2重解＋1つ別の解か3重解かはわからない。実数解3つであることは確定。） D

高校数学 3次関数に引ける接線の本数 領域の図示 受験の月

数学 B 3次方程式が2重解をもつ条件 学習院大 聖マリアンナ医科大 自治医科大 大学入試数学の考え方と解法

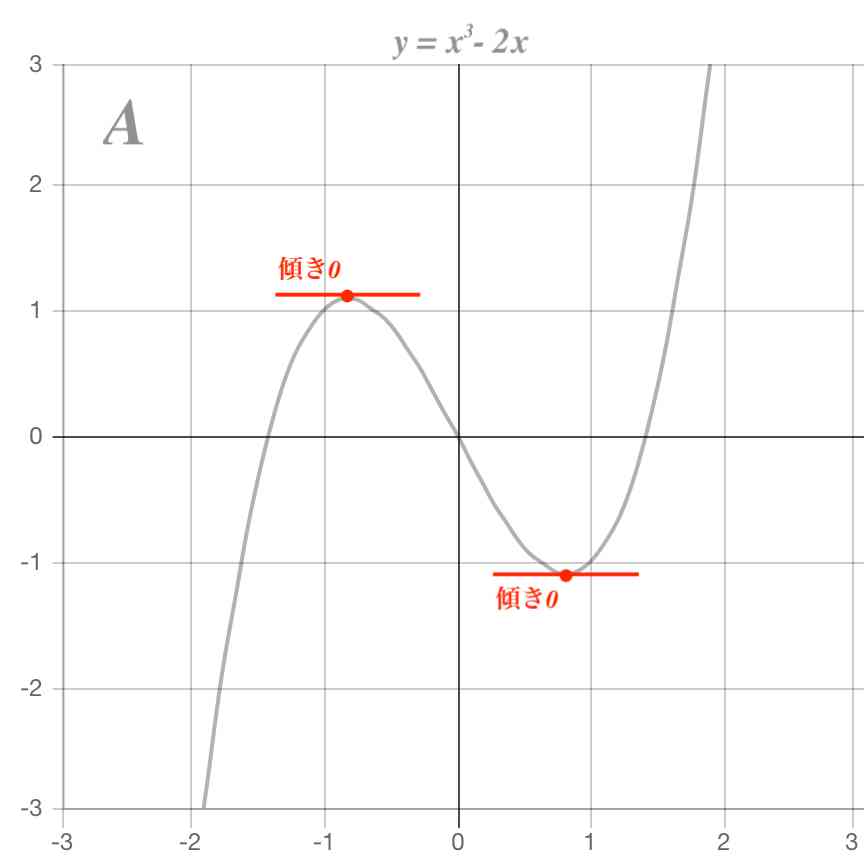
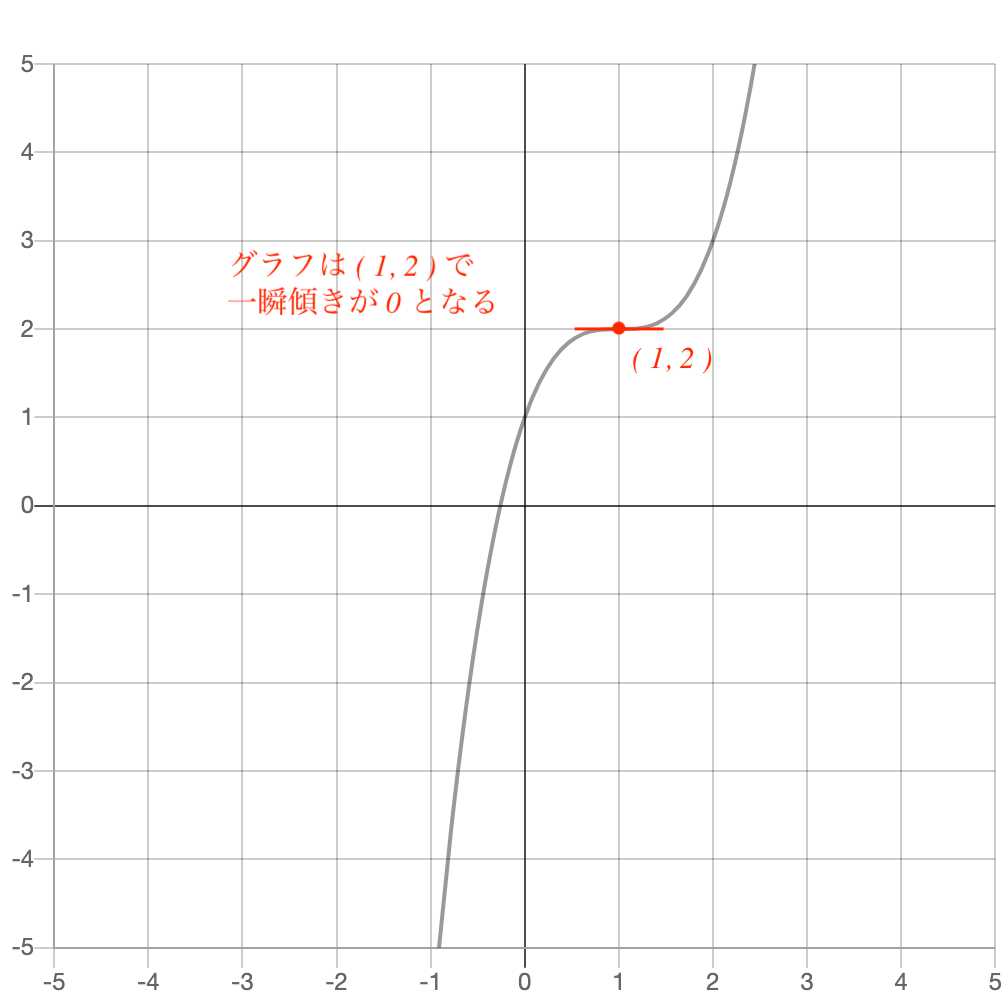
討した．第3学年の「関数y=ax2」単元で教材 「リレーのバトンパス」(大澤，1997)を扱い， グラフ描画ソフトGRAPES を活用した協働 的な解決，及び多様な解決方法の比較・検討 を重視して実践した．その結果，生徒は既習 の関数のグラフを用いた視覚的・近似なお、定義に従えば、y＝x 3 と x軸は原点において接している、とされます（グラフ的には交わっていますが） （補足）実際の「接する」関連の問題は、ふつう、以下のいずれかで扱う ・導関数などから接線を求める ・交点を求める方程式で重解 ・「2次Y' が重解を持つときは，その重なりに応じて 2重ならば2回変化（=変化なし），3重ならば3回変化（=1回変化）とする． 例と答 (1) y=3x 3 −9x 2 の増減を調べて極値を求めよ． （答案） y'=9x 2 −18x=9x(x−2) y'=0 となる x の値は， x=0 , 2

48s96ub7b0z5f Net Kyokuchi

３次関数 文字係数と極値

練習問題3問を解いてみよう さて、ではまず重解の問題に慣れるために、いくつか基本問題を解いていきましょう。 問題1．次の問いに答えなさい。 (1) 二次方程式 x 2 6 x 9 = 0 x 2 6 x 9 = 0 の重解を求めなさい。 (2) 二次方程式 3 x 2 2 x k = 0 ① 3 x 2 2 x k = 0 ① が重解を持つように、 k k の値を定めなさい。 (3) 二次関数 y = x 2 − 2 k k y = x 2 − 2 k k の Top / 線形代数I / 広義固有空間の構造とジョルダン標準形;(月) (97d) 更新 印刷しないセクションを選択

三次関数のグラフと極値の求め方 問題の解き方を解説 数学2 微分

1

 なお3次関数を\( f(x)=ax^3bx^2cxd \)とおきます。 a>0 or a0のときは右肩上がりの3次関数 ・a1 次の問いに答えよ． (1) 関数y = x 7 x 3 x2 の増減と極値を調べ，グラフの概形をかけ． (2) 3 次方程式x3 ax2 7x 3 = 0 が相異なる3 つの実数解をもつような実数a の値の範囲を求めよ．また，この方程式が重解をもつときの実数a の値とそのと きの解を求めよ．− 81 − 高校講座・学習メモ 数学Ⅰ 2次関数のグラフと2次方程式 例えば、 2x 2 －3x－4＝0を考えると、解の公式を用いて、

方程式の解の個数の問題が分かりません 写真のような問題と解説があるので Okwave

二次方程式の虚数解を見る むいしきすうがく

問題例 条件 解とグラフの位置関係 ⑩と同じ。ただし, 頂点の y 座標≦0となる。 ⑫と同じ。ただし, 頂点の y 座標≦0となる。 2つに場合 分けする！ 2つに場合 分けする！ ① ② ③ ④ ⑤ ⑥ ⑦ ⑧ ⑨ ⑩ ⑪ ⑫ ⑬ 図1 図2 図3 重解も含む 接する場合 ともに正。 ベストアンサー：3重解と1重解があるのは，5次方程式の場合です。 3＋2＝5 2つの接点というのは，それぞれ重解以上ということで あり， 4次方程式の場合は，2つの重解の場合しか三次方程式 a x 3 b x 2 c x d = 0 ax^3bx^2cxd=0 ax3 bx2 cx d = 0 の解を α, β, γ \alpha,\beta,\gamma α,β,γ とおく。 このとき，判別式を， D = a 4 ( α − β) 2 ( β − γ) 2 ( γ − α) 2 D=a^4 (\alpha\beta)^2 (\beta\gamma)^2 (\gamma\alpha)^2 D = a4(α −β)2(β −γ)2(γ −α)2 とする

三次関数と直線が接する 重解 参考書でa B C は実数としてf X X 3 A 数学 教えて Goo

高校数学 第２次導関数と極値 映像授業のtry It トライイット

⋆ べき関数の逆関数 べき関数y = xn (x 2 R) の逆関数を考える。 n = 2m が偶数のときは、y = x2m はR 上1 対1 ではないが、0;1) 上に制限すれば、1 対1 (狭義単調 増加) となる。 y = x2m (x 2 0;1)) x = y2m1 (y 2 0;1)) ここで、a > 0;もう1つの例として、微分後の関数 y' が重解を持つ場合のグラフについてもみていきましょう。 y = x 3 3x 2 3x 1 この関数のグラフを書いていきたいと思います。 まず、この関数を微分してみます。 y' = 3x 2 6x 3 微分の後、因数分解すると、 y' = 3 ( x 2 2x 1 ) 1年以上前 極値とは、傾きが⇔＋に入れ替わる点のy座標です。 重解だと傾きは＋or－のままなので極値を持ちません。 例としてy＝x³のグラフをのせておきます。 ゲスト 1年以上前 y=x^46x^28x3 のグラフで私は赤線のように書いてしまったのですが、何故

三次関数とは グラフや解き方 接線 極値の求め方 微分 受験辞典

三次関数のグラフと極値の求め方 問題の解き方を解説 数学2 微分

小野測器減衰をあらわす係数の意味と求め方 (page2) 3 減衰の効果 ここまでは、振幅が指数関数的に減衰していく状態を前提に減衰比や損失係数の求め方について説明しましたが、ここからは減衰比が実際の振動で物理的にどのような意味を持つかについて \(x^37x^215x9=0\)を\((x1)\)で割ると、 \((x1)(x^26x9)=0\)となり、 二次の部分をさらに因数分解をすると、\((x1)(x3)^2=0\)となります。 よって、三次方程式\(x^37x^215x9=0\)の解は、\x=1とx=3(重解)\となります。 グラフの形状の把握に使う。 は、 の極値 に対して、 で算出される値で、これも判別式として利用する。x軸との交差回数の判定のために使います;

三次関数のグラフと極値の求め方 問題の解き方を解説 数学2 微分

3次方程式の解の個数問題 数学の偏差値を上げて合格を目指す

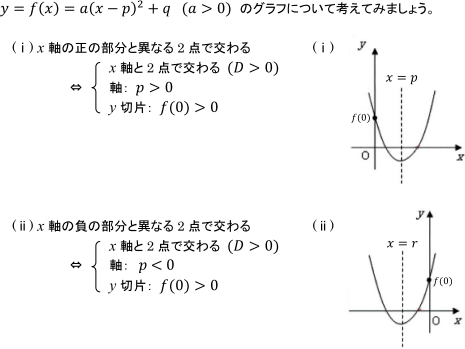
できれば，グラフを書かずに，y=ax2bxc の係数 a,b,c だけを見ることにより，上の3種類のうちのどの状態になっているのか判別してみようということです。 そのため，まず，①②③に書かれている条件を式に置き換えてみることにします。 初めに，y=ax2bxc (a>0) の頂点を求めることにしましょう。 少しややこしい変形ですが，右の式を見て考えてください。 この式2次関数や3次関数のグラフはだいたいの形が決まっていますが, 複雑な関数のグラフは, 増減だけでは正確な形がわかりません。それでは, 増減のほかに何を調べたらよいか, 具体的な例を見てみましょう。 これより, y の増減表は次のようになります。 この3次関数のグラフをかく手順は 6通りごとに増減表を考えると 単調増加、または単調減少なので極値が 存在しない。 y f x がx 軸と接する、または共有点 を持たない。 つまりf x が重解を持つ、または実数 解を持たない（虚数解を持つ）。

極値 極大値 極小値 を持つ条件と持たない条件

三次関数とは グラフや解き方 接線 極値の求め方 微分 受験辞典

 D や 4 分の D の公式、グラフと解の範囲 判別式 の値が のとき 、実数解の個数は 個、すなわち 重解 をもちます。 二次方程式 の解 x = \displaystyle \frac {− b \pm \sqrt {D}} {2a} について、 D > 0 のとき \sqrt {D} は実数、よって実数解は x = \displaystyle \frac {− b \sqrt {D}} {2a}, \frac {− b − \sqrt {D}} {2a} の 2 つ D = 0 のとき

Www Mathema Jp Wp Content Uploads 17 11 4e0b4a9bde1b6591c4bbe372aa2677 Pdf

重解の求め方とは 二次方程式が重解をもつ条件を解説します 遊ぶ数学

3分で分かる 重解とは何かを様々な角度から解説 合格サプリ

１次関数３ １次関数のグラフの交点と連立方程式の解 身勝手な主張

2

1

微分で 重解を持つときはなぜ極値をもなないのでしょうか 詳しくお願いします Clear

うさぎでもわかる線形代数 第22羽 ジョルダン標準形 工業大学生ももやまのうさぎ塾

三次関数のグラフの書き方

重解とは 求め方 絶対解きたい超頻出の問題付き 高校生向け受験応援メディア 受験のミカタ

三次関数のグラフの書き方

1次関数と2次関数の接点 タカラゼミ

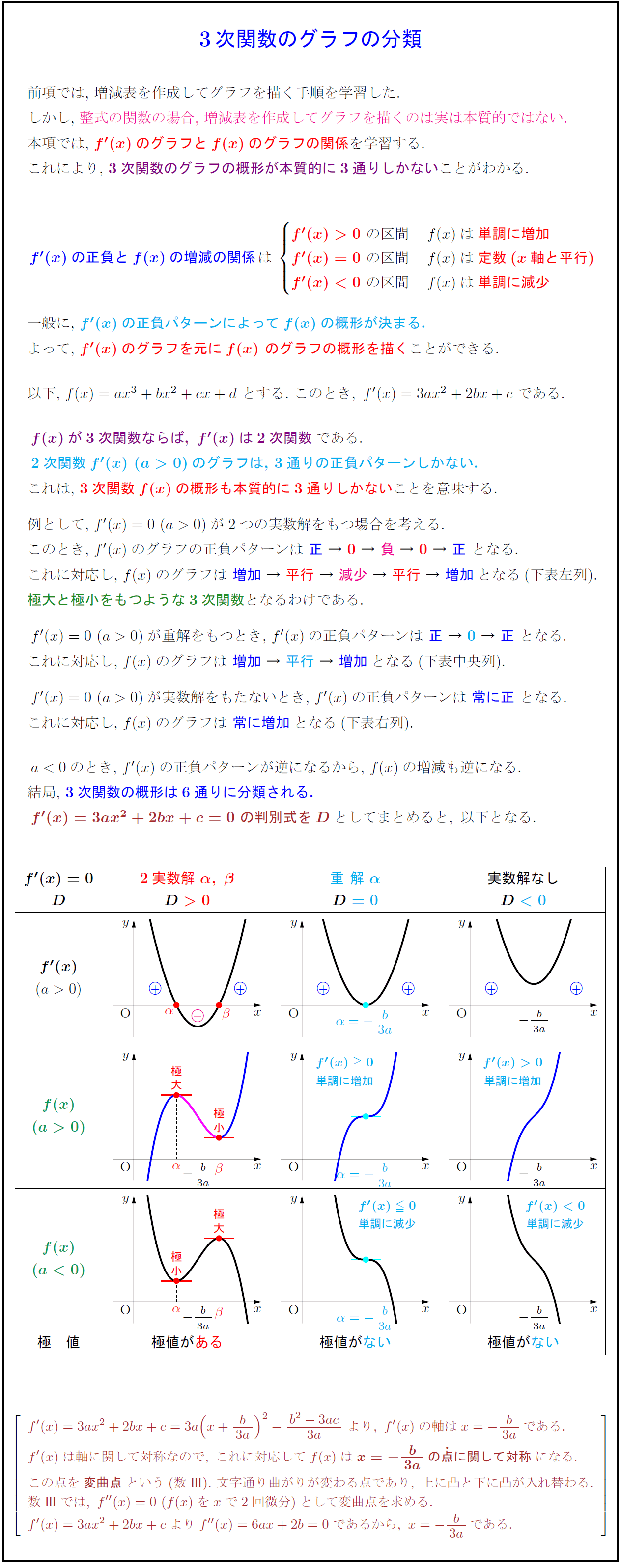
高校数学 3次関数のグラフの分類 F X のグラフとf X のグラフの関係 受験の月

なぜ76の方はあれで答え終わりなのに77は2を付け加えるんですか なんの違いで Clear

三次関数と直線が接する 重解 参考書でa B C は実数としてf X X 3 A 数学 教えて Goo

三次関数のグラフの書き方

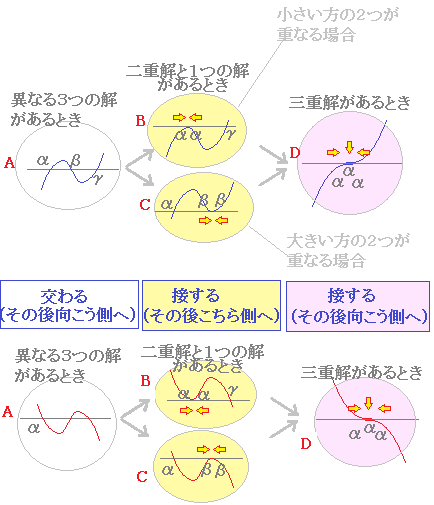
３次関数のグラフ

三次関数のグラフと極値の求め方 問題の解き方を解説 数学2 微分

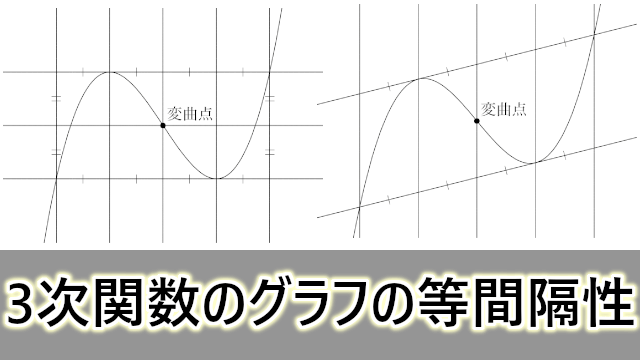
3次関数のグラフの等間隔性 大学入試数学の考え方と解法

多項式関数のグラフで直線と接する 重解となるのはどうしてです Yahoo 知恵袋

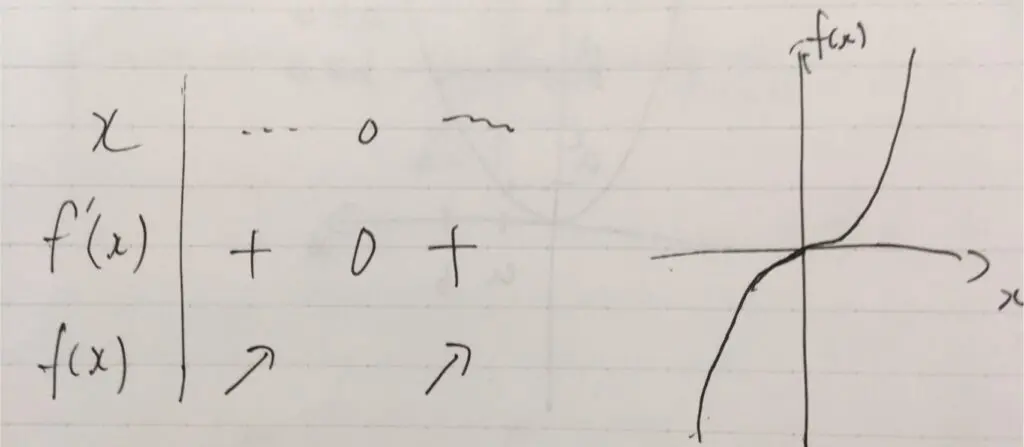
極値の求め方と判定条件 具体例と注意点 趣味の大学数学

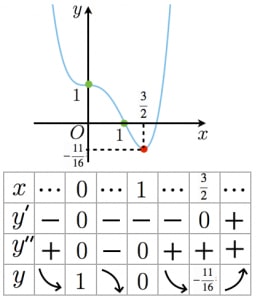
四次関数の二重接線を素早く求める方法 高校数学の美しい物語

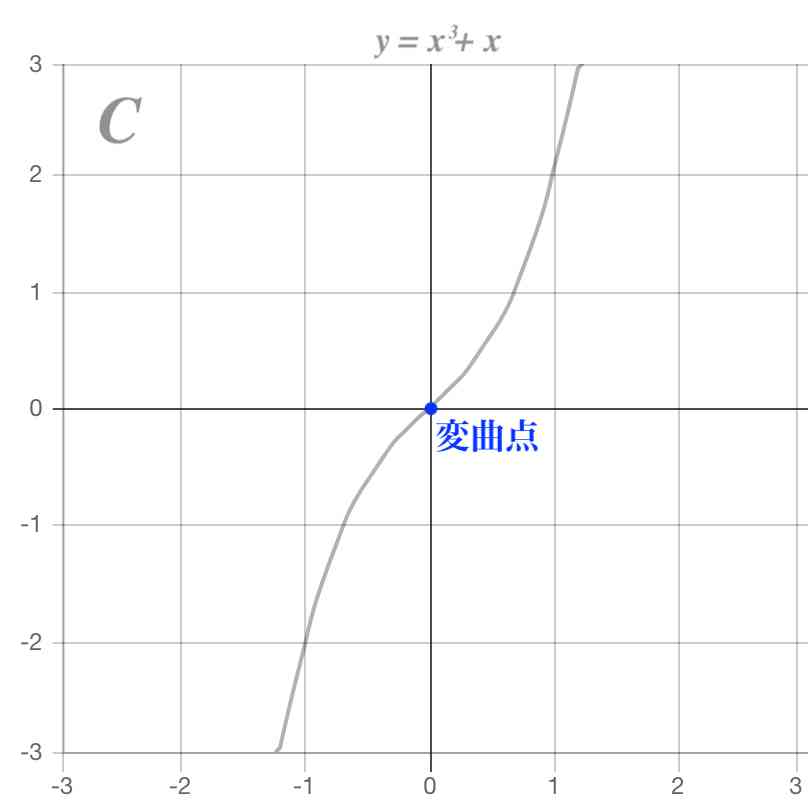
三次関数のグラフの書き方

2

高次方程式 数学ii フリー教材開発コミュニティ Ftext

杜陵サークル２月例会案内

極値を持つ 持たない 条件の判別式を用いた求め方とは 他の応用問題アリ 遊ぶ数学

高校数学 4次関数のグラフの図示 受験の月

3分で分かる 重解とは何かを様々な角度から解説 合格サプリ

三次関数のグラフと極値の求め方 問題の解き方を解説 数学2 微分

なぜf X が重解を持つとき F X のグラフはx軸と接するん Yahoo 知恵袋

極値を持つ 持たない 条件の判別式を用いた求め方とは 他の応用問題アリ 遊ぶ数学

3 です 表の矢印の向きって重解の時は全部同じじゃないんですか Clear

4次方程式 解説してほしいです Okwave

２次関数 ２次関数のグラフとx軸との位置関係について 日々是鍛錬 ひびこれたんれん

2

三次方程式で異なる三個の実数解とありますが 重解ということはあり得 高校 教えて Goo

三次関数と直線が接する 重解 参考書でa B C は実数としてf X X 3 A 数学 教えて Goo

標準 四次関数と微分 なかけんの数学ノート

X 0だとなぜ極大値がないと言えるのですか Clear

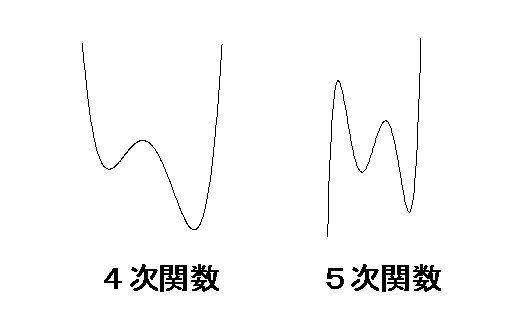
四次関数のグラフの概形と例題２問 高校数学の美しい物語

3次方程式の解の個数問題 数学の偏差値を上げて合格を目指す

二次方程式の虚数解を見る むいしきすうがく

三次関数とは グラフや解き方 接線 極値の求め方 微分 受験辞典

３次関数のグラフ

高校数学 直線と放物線の共有点の分類 映像授業のtry It トライイット

2 です 三次関数が3つの実数解をもつときのグラフにおける範囲はどう Yahoo 知恵袋

4次関数の問題で 極大値を持たないということは負から正の符号変化がないの Yahoo 知恵袋

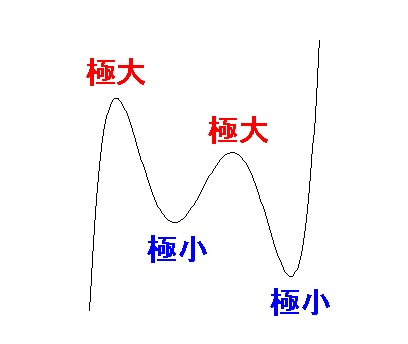
極値 極大値 極小値 を持つ条件と持たない条件

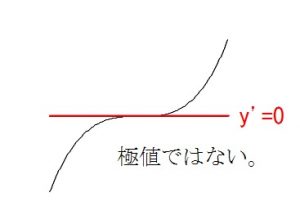
極値 極大値 極小値 を持つ条件と持たない条件

2次不等式

三次関数とは グラフや解き方 接線 極値の求め方 微分 受験辞典

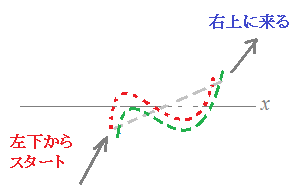
３次関数のグラフ

極値を持つ条件 数iii範囲 数学の偏差値を上げて合格を目指す

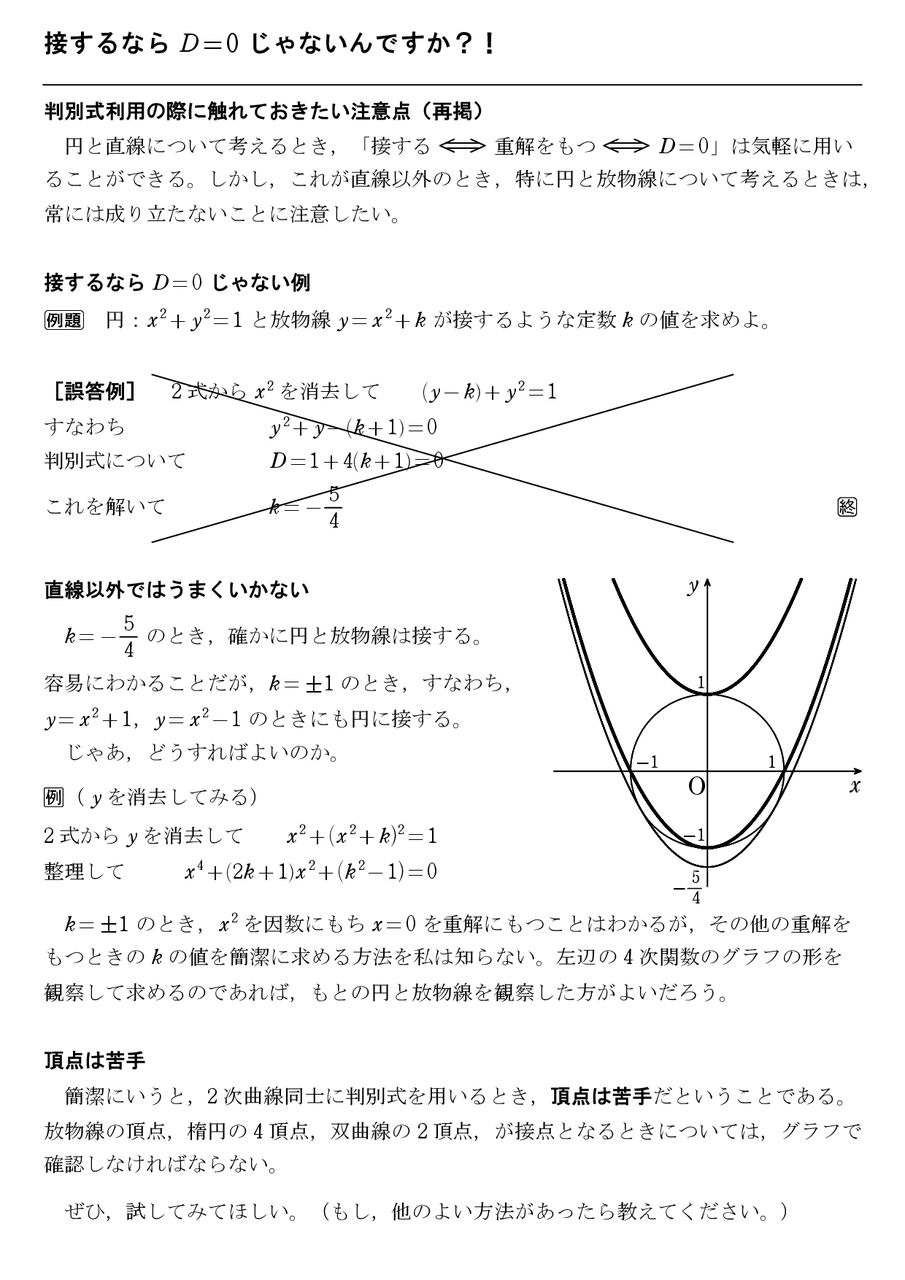
接するならd 0じゃないんですか 怜悧玲瓏 高校数学を天空から俯瞰する

微分で 重解を持つときはなぜ極値をもなないのでしょうか 詳しくお願いします Clear

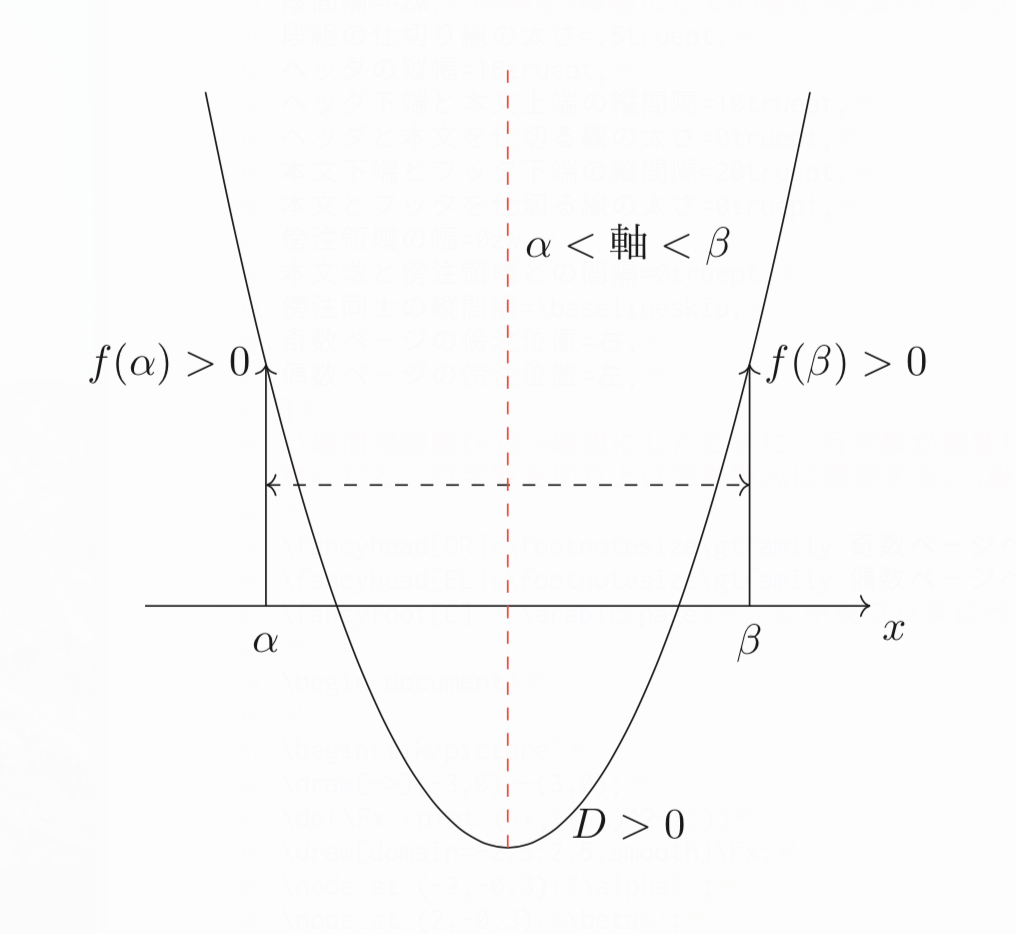
解の配置問題のパターンや解き方を例題付きで東大医学部生が解説 東大医学部生の相談室

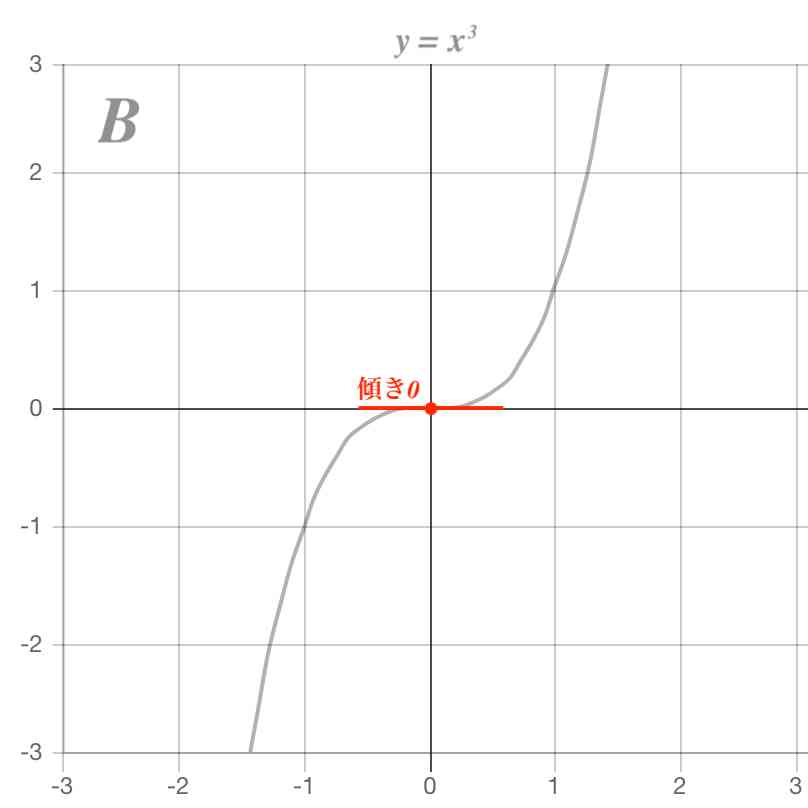
三次関数のグラフの書き方

三次関数とは グラフや解き方 接線 極値の求め方 微分 受験辞典

高校数学微分 この問題の 2 の答えが K 5と27なの Yahoo 知恵袋

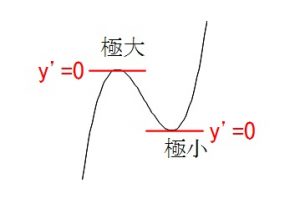
極値 極大値 極小値 を持つ条件と持たない条件

三次関数のグラフの書き方

3分で分かる 重解とは何かを様々な角度から解説 合格サプリ

極値 極大値 極小値 を持つ条件と持たない条件

1 次の問いに答えよ 1 関数 Y X 7 X 3 X2 の増減と極値を調べ グラフの概形をかけ 2 3

Q Tbn And9gcrgpzd6zrnsfvmnyzeksxevrtufuxjv2q6waxpw9rngtt04aulp Usqp Cau

48s96ub7b0z5f Net Kyokuchi

三次関数の重解とグラフについて三次関数が重解を持つとき 重解がグラフでは Yahoo 知恵袋

極値を持つ 持たない 条件の判別式を用いた求め方とは 他の応用問題アリ 遊ぶ数学

高校数学 3次関数の極値から係数決定 受験の月

極値 極大値 極小値 を持つ条件と持たない条件

円と放物線が接する 重解 Accademia Nuts

3

三次関数のグラフの書き方

２次関数 ２次方程式の解の存在範囲と判別式 数学 定期テスト対策サイト

３次方程式を解け ２重解 ３重解 一夜漬け高校数学242 高次方程式 Youtube

3次方程式の解の個数問題 数学の偏差値を上げて合格を目指す

三次関数とは グラフや解き方 接線 極値の求め方 微分 受験辞典

３次関数の増減 文字係数

1 X Af X Yi 2leqxleq2 Descubre Como Resolverlo En Qanda

極値 極大値 極小値 を持つ条件と持たない条件

重解を持つ三次関数のグラフってどんな感じになりますか Yahoo 知恵袋

四次関数のグラフの概形と例題２問 高校数学の美しい物語

三次関数とは グラフや解き方 接線 極値の求め方 微分 受験辞典

Incoming Term: 3重解 グラフ,